Understanding the Discriminant of a Quadratic

This seems to be a topic that repeatedly challenges A-level Maths students in their AS year. Often, not enough time is spent really thinking about what the discriminant reveals. This short article will hopefully lay it all out clearly.

What is it? Simply, it is \(b^{2}-4ac\). This is a function of the coefficients of a quadratic in general form \(ax^2+bx+c=0\). The discriminant is a tool that helps to know the properties of the roots/solutions without having to calculate them. Most students either were not taught or don't know where it comes from. It comes from the quadratic formula, and if you haven't had it explained before, the quadratic formula is the completed square form, with \(x\) the subject, of the general form for a quadratic \[x=\frac{-b\pm \sqrt{b^{2}-4ac}}{2a}\]It's a good test of your completing the square skills to see whether you can work it through to obtain the quadratic formula.

At GCSE you were hopefully taught to use the quadratic formula to find roots/solutions to a quadratic function if you can't factorise it, but you were not likely taught anything else about it. Just another formula to remember. If we take a closer look there is more to glean.

As said before, it gives us roots/solutions to our general form of the quadratic, which is dependent on the values of \(a\), \(b\) and \(c\). Further inspection shows the value of \(x\) depends on the square root term which has two possible values that come from the \(\pm\) sign. Possible, because it is limited by the value of the terms inside the square root. These terms, \(b^2-4ac\) (the discriminant), are the overall cause of the properties of the roots/solutions to the quadratic. By looking generally at the values of the discriminant, and general because we don't have any actual numbers, we can arrive at an understanding of the properties of the roots/solutions. There are three possible outcomes for the value of the discriminant, which in turn create the possible roots/solutions/values of \(x\):

  • If \(b^2-4ac>0\) the value of the square root will be positive, which in turn means the \(\pm\) sign is included in the overall evaluation of \(x\). Therefore, \(x\) has two real solutions.
  • If \(b^2-4ac=0\) the value of the square root is zero, leaving the term \(\frac{-b}{2a}\) . So there can be only one real solution for \(x\). This is also known as a repeated root.
  • If \(b^2-4ac<0\) then we will have to evaluate square root a negative number. We are all told, perhaps up until this point in our maths education, that you can't take a square root of a negative number. The answer is true in the context of what you have learnt so far, which is that you can't make a negative number by multiplying a negative real number by itself. You may not have heard of a real number, but this is likely because there has been no context for it. The real number is contrasted with the complex number, which is a number that you can multiply by itself to make a negative number. This created a whole new branch of mathematics, complex number theory, in order to be able to solve problems that can't only be solved with real numbers. So in this case, although we can't evaluate the square root of a negative number, our square root is still evaluated with the \(\pm\) sign. So the solution to \(x\) also has two solutions. However, they are not real numbers but complex numbers. And so, we say that \(x\) has two complex roots/solutions.

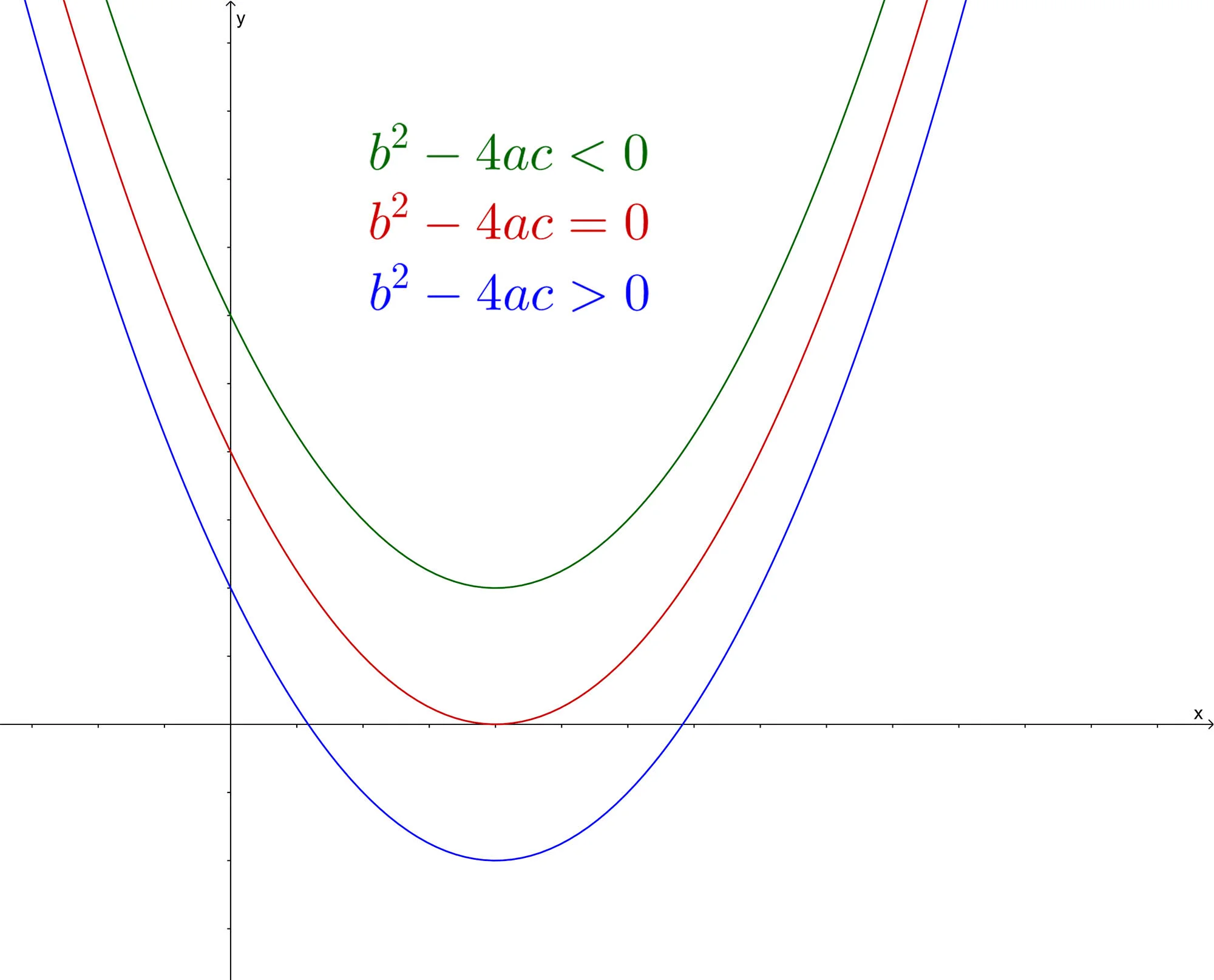
Whilst we're here, it's worth having a look at what each of these cases will look like graphically. The roots/solutions are the \(x\)-values of the function where it crosses the \(x\)-axis, or alternatively, when \(y=0\).

 
Discriminant
 
  • You may be inclined to think that when the quadratic goes below the \(x\)-axis (blue curve) that \(b^{2}-4ac<0\). Have a closer look. When the quadratic is below the \(x\)-axis there a clearly two points where the function crosses the \(x\)-axis, therefore there are 2 distinct real roots i.e. \(b^{2}-4ac>0\).
  • For the graph of the function that only touches the \(x\)-axis in one place (red curve), the answer should be obvious, it correlates to \(b^{2}-4ac=0\), one real solution or a repeated root.
  • And when the curve does not touch the \(x\)-axis (green curve) there can be no solutions/roots, which correlates with \(b^{2}-4ac<0\), complex roots/solutions

When looking at a graph, think of how many solutions you see and reference those with either of the three discriminant cases and you will be spot on. Don't make the mistake of correlating the discriminant with whether the curve is above or below the \(x\)-axis.

Gravity on Comet 67P/Churyumov–Gerasimenko

Comet 67P/Churyumov–Gerasimenko - On Rosetta's approach to the comet. Yes, this is a real picture as fantastic as it is.

Comet 67P/Churyumov–Gerasimenko - On Rosetta's approach to the comet. Yes, this is a real picture as fantastic as it is.

Comet 67P/Churyumov–Gerasimenko (67P/C-G) is a comet whose orbit extends as far out as the orbit of Jupiter but comes as close as to between the orbits of Earth and Mars. Its year, or orbit, is 6.44 years and its day, time for one rotation, is 12.4 hours. It was first discovered in 1969 by astronomer Churyumov from a photographic plate taken by the astronomer Gerasimenko, hence the name. In 2004 the spacecraft Rosetta along with its lander module Philae left Earth on a 10 year trip to the comet in order to make a detailed study. It is the first mission to land a space probe, Philae, on the surface of a comet.

The Hathor region of comet 67P/C-G - The cliff on the right of the image is about 923m high. This is slightly larger than the rock face of the climbing route called The Nose on El Capitan in Yosemite National Park

The Hathor region of comet 67P/C-G - The cliff on the right of the image is about 923m high. This is slightly larger than the rock face of the climbing route called The Nose on El Capitan in Yosemite National Park

A fun question came up recently, which was if i hitched a ride on Rosetta and Philae, how much would i weigh on the comet and could i walk around on it? Or even, if i jumped off this cliff on the Hathor region, which is approximately 923 metres high (see image on the left), what would happen? An awesome cosmic base jump or a gentle float to the bottom?

Below, i go through the calculations that are approachable for an A-Level Physics student in their A2 year. You can decide whether you think the result exciting, surprising or disappointing.

Weight on Comet 67P/C-P

To find our weight on 67P/C-G we need to know the gravitational field strength of the comet. Given that the comet is not really close to spherical it does make the problem considerably more difficult as one would have to model the gravitational field profile for the comets double lobe shape, which has been done here. To make this a more digestible problem we will assume the comet has spherical symmetry and treat it has having a point mass so we can easily use Newton's Law of Gravitation. So to start with, to find the gravitational field strength of an object on the comet, we can equate the forces of weight with the force between two point masses (Newton's Law of Gravitation). The equation for weight is \[F=mg_{67P}\] where \(F\) is the force of the object's weight on the surface of the comet, \(m\) is the object's mass and \(g_{67P}\) is the gravitational field strength of the comet. The equation for the force between the object's mass and the comet's mass is \[F=\frac{Gmm_{67P}}{r^2}\] where \(G\) is the gravitational constant, \(m\) is the object's mass, \(m_{67P}\) is the comet's mass and \(r\) is the radius of the comet. Equating these two equations gives \[mg_{67P}=\frac{Gmm_{67P}}{r^2}\]The object's mass \(m\) is common on both sides and so cancels giving \[g_{67P}=\frac{Gm_{67P}}{r^2}\]We now have a formula for the gravitational field strength of comet 67P/C-G. Notice that this does not depend on the mass of whatever object might come into the influence of the comet's gravitational field. It is only dependant on the Gravitational constant (which itself is constant), the mass of the comet (which in this case is also constant) and the radius (which is how far we are from the centre of the sphere when standing on the surface). To find a value for \(g_{67P}\) we need values for all three. The Gravitational constant is \(G=6.67×10−11\rm Nm^{2}kg^{−2}\) and the comet's mass is quoted as approximately \(m_{67P}=9.98\times 10^{12}\rm kg\). The value for the radius takes a little more work as we have essentially imagined the comet being melted down and reformed as a perfect sphere. To find the radius we can work backwards from the volume of a sphere \[V=\frac {4}{3}πr^3\]and rearrange for the radius \[r=\sqrt[3]{\frac{3V}{4\pi }}\]Now we just need a volume estimate of our reformed comet, which comes in at \(V=1.87\times 10^{10}\rm m^3\). In turn this gives us a rough value for the radius of \[r=\sqrt[3]{\frac{3\times 1.87\times 10^{10}}{4\pi }}=1646\rm m\]We now have what we need to find the gravitational constant of \(g_{67P}\). Finally putting this all together using all of our three values, we get \[g_{67P}=\frac {6.67\times 10^{−11}\times 9.98\times 10^{12}}{\left (1646 \right )^{2}}=2.46\times 10^{−4}\rm ms^{−2}\]What does this tell us? Well, by comparing with the gravitational field strength on Earth \(g_{\bigoplus }=9.81\rm ms^{−2}\) we can see that comet 67P/C-G has a gravitational field strength that is smaller by a factor \[\gamma =\frac {9.81}{2.46×10−4}=39878\]So, as for my weight on the comet, i'd be about 40000 times lighter. For a \(70\rm kg\) man, like myself, that would be equivalent to \[\frac {70}{39878}=1.76\times 10^{−3}\rm kg=1.76g\]In short, really not a whole lot. To compare, a 5 pence coin on Earth weighs more, at \(3.25\rm g\). So my weight would be a little more than half of a 5 pence coin. Theoretically i could stand on the comet but the tiniest movement of the muscles in my legs, which are easily capable of exerting forces tens of thousands of times that of the weight of a 5 pence coin, will cause me to leave the comet's surface. Walking would be an incredibly delicate process.

Jumping off Hathor Cliff

As for our question of base jumping off the Hathor cliff, you can probably guess that this is going to take a while with such little gravity. Certainly jumping up and out from the top of the cliff would be out of the question as this would sent us into space. Once standing on the edge, we would simply have to allow ourselves to fall. We can use Newton's kinematic equations to work out a time of flight and how fast we might be travelling when we hit the ground. My initial speed is \(u=0\rm ms^{−1}\), the distance i travel is \(923\rm m\) and the acceleration is the gravitational field strength of the comet \(g_{67P}=2.46\times 10^{−4}\rm ms^{−2}\). Taking downwards to be the positive direction and using \[s=ut+\frac{1}{2}at^2\]when \(u=0\) gives \[s=\frac{1}{2}at^2\]Now rearrange for \(t\) and input our values \[t=\sqrt{\frac{2s}{g}}=\sqrt{\frac{2\times 923}{2.46\times 10^{-4}}}=2739\rm \: seconds\] A little over 45 minutes, which is rather a slow trip. Not one i would likely call a base jump, but if a float is what you're after then comet 67P/C-G is for you. As for the speed we would hit the ground, we can use \[v=u+at\]with \(u=0\) so \[v=at=2.46\times 10^{-4}\times 2739=0.67\rm ms^{−1}\]which is a speed of 67 centimetres every second. This certainly is an impact that the body could handle. So all in all, parachutes would not be needed and we could perhaps jump all the way back to the top. That problem, i leave for the reader.